What Is The Use of Trigonometry Calculator in Art & Design?

The use of trigonometry is extensive in the field of art and design. Even from ancient times, trigonometric shapes like triangles, pyramids, circles, and arches are used in various historical buildings. People are using trigonometric tools and equipment to measure the various lengths and angles in the architecture. In the modern era, the trigonometry calculator by calculator-online.net made it possible to construct the designer’s model and high-tech building. These buildings are the embodiment of the trigonometric and the art. Buildings like the Sydney harbor bridge, New York Hanging Bridge, and the Brug-ul-Arab are examples of trigonometry and measurements.

Architecture is used to decide the design of a building or a place, whether architects are able to construct it by using contemporary knowledge and skill. The Architecture applies the rules of trigonometry and measurements to construct various models. Trigonometry is the knowledge of the measurements and adjusting the material according to these specific measurements and angles. You can use trigonometric ratios like the “Sin”,”Cos” and “Tan” to find the various angles

This article discusses trigonometry and its uses in art and architecture.

What is trigonometry?

Trigonometry means the calculation and measurements of the triangle and the word tri is for the three. The trig calculator can be used to find the relationship between the various lengths, heights, and angles of a triangle. The trigonometric ratios are measurements that we use for the various measurements. The field of trigonometry is commonly used by architects, surveyors, engineering, and investigating. The trigonometry calculator makes it possible to apply the measurement accurately. When you are able to build a relationship between various lengths and their respective angles, then you are able to draw this shape practically in the field of art and design.

The history of trigonometry:

The history of trigonometry was used around 4000 years ago in the construction industry. The civilizations of Egypt, Mesopotamia, and India used the concept of trigonometry in their construction. Examples of trigonometry are the pyramids of the Gizza, the hanging gardens of Mesopotamia, and the Aha-Sofia of Constantinople. In recent times the Taj-Mahal was constructed by the Mughal emperor, you can say the rules of the trigonometric were used in the historical time in modern areas in art and industry. Trigonometric instruments were used by the architecture in the prehistoric and modern era.

How to use trigonometry in architecture?

There are various applications of trigonometry in the field of architecture and design. You can adjust the design and test the building loads before launching it on a practical level. This is done by the extensive testing of the design by the online trigonometry calculators and software. The art and design industry has grown to this level that we are able to adjust buildings to precise levels.

Trigonometry and slopes:

The major use of trigonometry is calculating the slopes and angles. When you are preparing a roof or arch, you need to calculate precisely what angle it should be, trigonometry is used to measure the slopes. Trigonometry is used to determine the various heights, slopes, angles, etc. You can use the trigonometry calculator to find the angles and ratio to use to level the roof or build the arch angle

Trigonometry and structural load

Trigonometry is also used to determine the structural load a building can bear. The whole design of the building is developed in a way to effectively lifts the load of the building. In the modern era, the hanging wire angle is adjusted by online software and a trigonometry calculator to lift the load. You actually adjust the load to a certain area at the building but keep a particular angle. You can adjust the structural load of a building by adjusting the various angles. For example, a certain slope of a wall or roof is used to cater a certain load.

Trigonometry and angles:

The trigonometry calculators are used to precisely draw the angle which provides precision to the building. The specific height of the building and the walls are adjusted to create the modern style of buildings. The test models are presented before construction and all the designs are tested by the online software. This is the main reason the architects are able to design various buildings which are astonishing in their architecture. Architecture is all about arranging various angles and shapes. When you are able to adjust the angles then you can merge them to present a certain shape or a design.

The basic of trigonometry:

The basis of trigonometry is based on the three sides of the triangle and their ultimate relation. The trigonometry calculator all the three trigonometric ratios and also the reverse trigonometric ratios of a triangle.

The Trigonometric Ratios:

The three sides of the triangle are the adjacent side, the opposite side, and the Hypotenuse. You can call the adjacent side as the base, and the opposite side as the perpendicular of a triangle. The basic trigonometric ratios are necessary to adjust when we are determining the angles of the various sides of the triangle. These sides may be hidden in a circle, pyramid, rectangle, or square.

The first trigonometric ratio is equal to the “Sin θ”

Sin(θ)= Opposite side /Hypotenuse

Sin(θ)= Perpendicular /Hypotenuse

The second trigonometric ratio is equal to the “Cos θ”

Cos(θ)= Adjacent side /Hypotenuse

Cos(θ)= Base /Hypotenuse

The third trigonometric ratio is equal to the “tan θ”

Tan(θ)= Opposite side /Adjacent side

Tan (θ)= Perpendicular /Base

These are the trigonometric ratios commonly used to find the angles between the three sides of the measurements. You can use the trig function calculator to adjust the length of various measurements by art and design when constructing a building or a site.

The reverse trigonometric ratios:

The reverse trigonometric ratios are also used in the various measurements of the construction. You may encounter the reverse trigonometric ratios when estimating the angles of a triangle hidden in circles, squares or the pyramid shapes

The first inverse ratio is Cosec(θ)

Cosec(θ) =Sin-1(θ)= Hypotenuse/Opposite side

Cosec(θ) =Sin-1(θ)= Hypotenuse/Perpendicular

The second inverse trigonometric ratio is equal to the “sec θ”

Sec(θ) =Cos-1(θ)= Opposite side/ Hypotenuse

Sec(θ) =Cos-1(θ)= Hypotenuse/Base

The third inverse trigonometric ratio is equal to the “Cot θ”

Cot(θ) =Tan -1(θ)= Adjacent side/ Opposite side

Cot(θ) =Tan -1(θ)= Base/Perpendicular

The trigonometric functions calculator can calculate the various measurements and their respective inverse angles. The basics for measuring and estimating the length of a side or eagle, we normally use the above-mentioned trigonometric ratios.

Trigonometry Use Cases

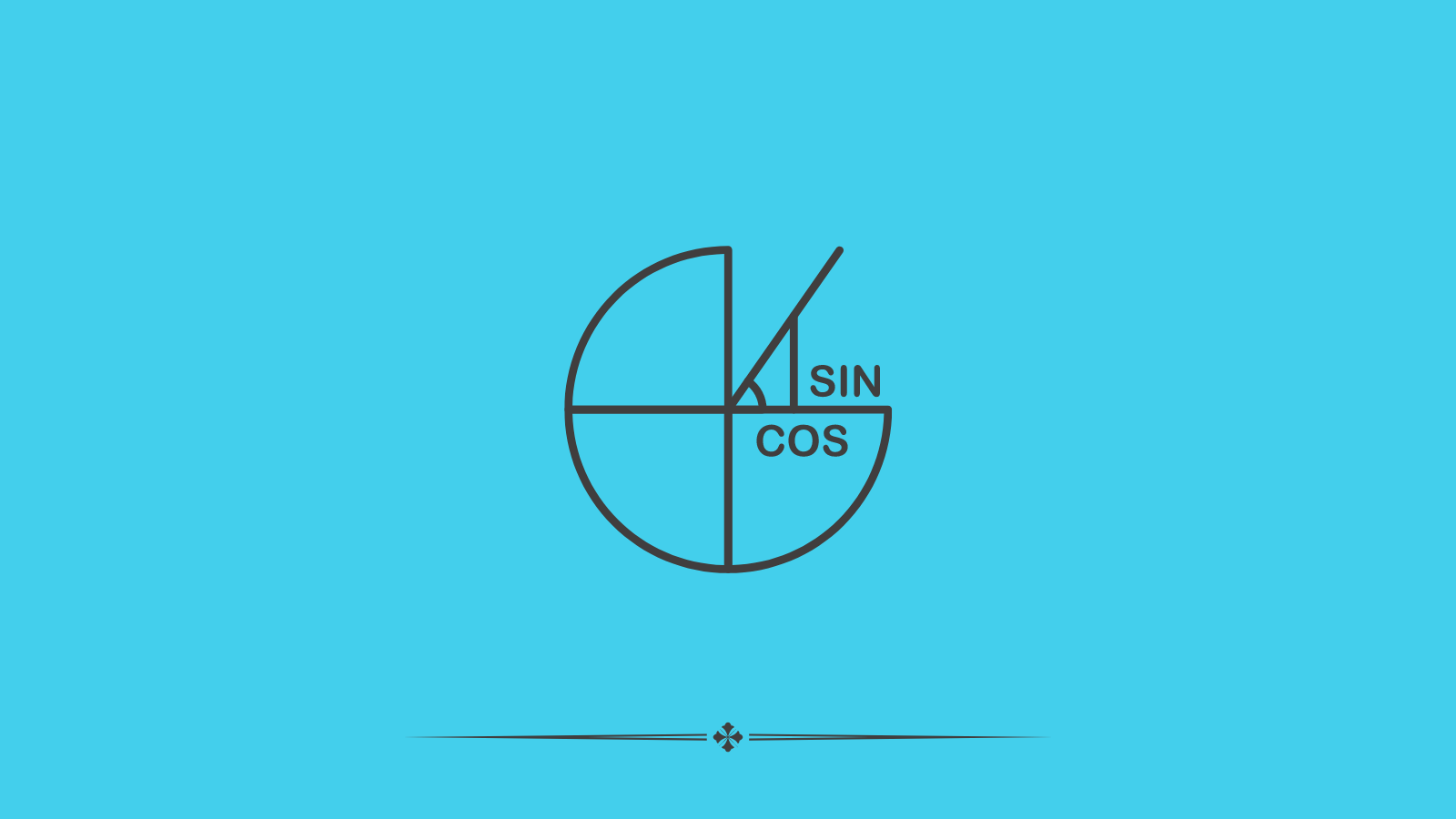
Trigonometry, the branch of mathematics that deals with the relationships between the sides and angles of triangles, has a wide range of practical applications across various fields. Below are some common use cases of trigonometry:

1. Architecture and Construction

Structural Design: Trigonometry is used to calculate angles, forces, and distances when designing structures like bridges, buildings, and tunnels. Architects and engineers use trigonometric functions to ensure that these structures are stable, safe, and balanced.
Roofing and Building Slopes: In construction, trigonometry helps determine the slope of a roof or ramp by calculating the angle of inclination based on height and length.
Blueprints and Measurements: Surveyors and architects rely on trigonometric calculations to interpret and create blueprints, ensuring accurate layout and dimensions.

2. Navigation

GPS Systems: Trigonometry is used in Global Positioning Systems (GPS) to determine the precise location of a point on Earth. The system calculates distances and angles between satellites and receivers to provide accurate coordinates.
Aviation and Marine Navigation: Pilots and sailors use trigonometry to calculate distances and angles when navigating routes. It helps determine position, direction, and distances over curved surfaces like the Earth’s surface, factoring in angles between the destination and the starting point.

3. Physics and Engineering

Wave Motion: In physics, trigonometry is used to analyze wave functions, such as sound waves, light waves, and electromagnetic waves. The sine and cosine functions model the periodic motion of these waves.
Forces and Motion: Engineers use trigonometry to resolve forces into perpendicular components. This is essential for understanding how objects move or how much force is exerted in a specific direction.
Projectile Motion: Trigonometry helps calculate the trajectory of objects launched into the air (e.g., projectiles, missiles). It is used to determine the range, height, and time of flight based on initial velocity and angle of launch.

4. Astronomy

Distance to Stars and Planets: Astronomers use trigonometry (parallax method) to calculate the distance to celestial bodies by measuring the angles between a star and two different points of observation (like Earth and a satellite).
Orbital Mechanics: Trigonometry is critical for determining the orbits of planets, moons, and artificial satellites. Calculations of angular velocity, eccentricity, and distance rely heavily on trigonometric principles.

5. Surveying and Land Measurement

Topographic Surveys: Surveyors use trigonometry to measure land distances and angles between different points to create accurate maps and models. Trigonometry helps determine elevations and plot the terrain.
Geodesy: This science involves measuring the Earth’s shape, orientation, and gravitational field. Trigonometry is used to calculate distances between geographic locations and the curvature of the Earth.

6. Computer Graphics and Animation

3D Modeling: In computer graphics, trigonometry helps render 3D objects by calculating the rotation, scaling, and translation of objects in space. It’s used to compute angles of light, shadows, and perspectives in animation.
Camera Angles: Animators and game developers use trigonometry to set camera angles, calculate movement paths, and create realistic simulations of environments.
Texture Mapping: Trigonometric functions help map textures onto 3D surfaces in games and animations, ensuring that they align properly as objects move and rotate.

7. Electrical Engineering

AC Circuit Analysis: Trigonometry is used to analyze alternating current (AC) circuits, which involve sinusoidal waveforms. Engineers use sine and cosine functions to model voltage and current in circuits and to calculate impedance, phase shifts, and power factors.
Signal Processing: Trigonometric functions are essential for analyzing and manipulating electrical signals in telecommunications, radio waves, and audio signals.

8. Medical Imaging

CT Scans and MRI: Trigonometry is used in computed tomography (CT) scans and magnetic resonance imaging (MRI) to reconstruct cross-sectional images of the body. The process involves calculating angles and slices based on X-ray or magnetic data.
Ultrasound: Trigonometry helps calculate the distance between the probe and the internal organs in ultrasound imaging, enabling doctors to see inside the body.

9. Robotics

Kinematics and Motion Control: In robotics, trigonometry is used to model and control the movement of robotic arms and joints. By calculating angles and distances, engineers can determine the position and orientation of each part in space.
Pathfinding and Navigation: Robots use trigonometry for pathfinding and obstacle avoidance. For instance, autonomous vehicles use trigonometric calculations to navigate routes and avoid collisions.

10. Music and Sound Engineering

Sound Waves: Sound engineers use trigonometry to model sound waves and determine how frequencies interact, such as in noise cancellation or equalization. Sine and cosine waves represent the oscillations of sound waves.
Audio Synthesis: Trigonometry is used in synthesizers to generate waveforms (sine, square, sawtooth) that produce different sounds in electronic music.

11. Criminology and Forensics

Accident Reconstruction: Forensic experts use trigonometry to reconstruct accidents by analyzing angles, speeds, and distances. For example, trigonometry helps determine the trajectory of projectiles or the angle of impact in a car crash.
Ballistics: In criminal investigations, trigonometry is used to calculate the trajectory of bullets, helping to establish the position of the shooter and the point of impact.

12. Sports and Athletics

Trajectory of Balls: In sports like basketball, golf, and soccer, trigonometry helps athletes and coaches analyze the trajectory of balls based on angle, velocity, and distance.
Optimal Angles: Trigonometry can be used to determine optimal angles for kicking, throwing, or hitting to achieve maximum range or accuracy.

Trigonometry plays a vital role in many fields, from engineering and science to entertainment and sports. Its ability to calculate angles, distances, and movements makes it a fundamental tool for solving practical problems in real-world applications.

Conclusion:

The trigonometric rules and ratios were commonly used in the art and construction industry since ancient times. Trigonometry is used at different levels in the art and design industry. You have various online software and trigonometry calculators to check the building design before implementation. This provides various options to engineers and artists, and you can see the amazing buildings being constructed around the world.

FAQ

What Is the Role of Trigonometry in Art?

Trigonometry plays a significant role in art, especially in creating accurate perspectives, proportions, and symmetrical designs, allowing artists to achieve realism and precision in their work.

How Does Trigonometry Help in Perspective Drawing in Art?

Trigonometry helps artists calculate accurate angles and dimensions for perspective drawing, creating the illusion of depth and three-dimensionality on a flat surface.

What Are Some Examples of Trigonometry in Artistic Creations?

Examples include Renaissance paintings with precise linear perspectives, Islamic geometric art patterns, and modern graphic designs that require complex shape calculations.

How Do Artists Apply Trigonometry in Sculpture?

In sculpture, trigonometry assists in scaling designs, ensuring proportionality, and in some cases, aiding in the construction of complex shapes and structures.

Can Trigonometry Be Used in Digital Art and Animation?

Yes, trigonometry is extensively used in digital art and animation for creating realistic movements, three-dimensional modeling, and camera angle calculations.

How Is Trigonometry Applied in Architectural Art?

In architectural art, trigonometry is crucial for designing structures, calculating slopes and angles, and ensuring that aesthetic elements of the design are proportionally and structurally sound.

What Is the Importance of Trigonometry in Mosaic Art?

Trigonometry is important in mosaic art for planning and executing patterns and designs that require precise angles and consistent shapes, especially in complex and large-scale works.

How Do Graphic Designers Use Trigonometry in Their Work?

Graphic designers use trigonometry to create layouts with precise alignment, to manipulate graphic elements, and in designing logos and visual elements that require geometric accuracy.

How Does Trigonometry Enhance Symmetry and Balance in Artistic Designs?

Trigonometry helps artists calculate precise angles and dimensions, ensuring symmetry and balance in designs, which is crucial for aesthetically pleasing and harmonious artworks.

What Role Does Trigonometry Play in Creating Optical Illusions in Art?

Trigonometry is instrumental in creating optical illusions, as it allows artists to manipulate angles and perspectives to trick the eye, creating images that seem to move or have hidden elements.

Can Trigonometry Be Used in Photographic Composition?

In photography, trigonometry aids in calculating perspective, depth of field, and camera angles to achieve desired compositions and capture images with accurate spatial representation.

How Is Trigonometry Applied in the Creation of Tessellations in Art?

Trigonometry is used in designing tessellations to ensure that shapes fit together perfectly without gaps or overlaps, creating seamless and often intricate repeating patterns.

What Is the Historical Significance of Trigonometry in Artistic Movements?

Historically, trigonometry has been significant in movements like the Renaissance, where artists like Leonardo da Vinci used mathematical principles to revolutionize perspective in art.

How Do Street Artists Use Trigonometry in Their Murals?

Street artists use trigonometry to scale their designs correctly, especially for large murals, ensuring that proportions are maintained and the final artwork aligns with their initial vision.

Can Trigonometry Assist in Light and Shadow Calculations in Art?

Yes, trigonometry assists in calculating the angles and distances for light sources in art, helping artists depict realistic shadows and lighting effects.

How Is Trigonometry Relevant in Kinetic and Geometric Art?

In kinetic and geometric art, trigonometry is essential for designing moving parts that function correctly and for creating artworks based on geometric shapes and patterns.

What Are the Benefits of Using Trigonometry in Installation Art?

For installation art, trigonometry ensures that structural elements are correctly proportioned and balanced, especially for large or complex installations that interact with their environment.

How Do Fashion Designers Utilize Trigonometry?

Fashion designers use trigonometry to calculate angles and curves for garment patterns, ensuring a precise fit and creating designs that require geometric precision.

How Does Trigonometry Aid in the Creation of 3D Art and Sculptures?

Trigonometry helps artists and sculptors calculate precise dimensions and angles for 3D artworks, ensuring accurate representation of depth and perspective.

Can Trigonometry Be Used to Replicate Historical Art and Architectural Styles?

Yes, trigonometry can be used to accurately replicate historical art styles and architectural designs, particularly those that involve complex geometric patterns or structures.

How Do Filmmakers Utilize Trigonometry in Their Work?

Filmmakers use trigonometry to plan camera angles, movements, and special effects, ensuring that visual elements are proportionally correct and visually appealing.

What Is the Role of Trigonometry in Stage Design and Theater?

In stage design, trigonometry is used to create sets with accurate perspectives and dimensions, enhancing the visual storytelling of theater productions.

How Can Trigonometry Improve the Accuracy of Proportions in Portraiture?

Trigonometry allows artists to calculate exact proportions and angles in portraiture, ensuring a more lifelike and proportionally accurate depiction of the subject.

Are There Specific Artistic Techniques That Rely Heavily on Trigonometry?

Techniques like anamorphosis (creating distorted images that appear normal from a specific angle) and trompe-l’œil (optical illusion in art) rely heavily on trigonometry for their effectiveness.

How Is Trigonometry Used in Digital Graphic Design and Animation?

In digital design and animation, trigonometry is used to create and manipulate geometric shapes, control animation paths, and simulate real-world physics.

Can Trigonometry Be Applied in Traditional Crafts and Textile Design?

Yes, trigonometry can be applied in crafts and textile design, particularly in creating patterns, weaving, and ensuring symmetrical designs.

What Impact Does Trigonometry Have on Visual Composition in Art?

Trigonometry allows artists to create compositions with balanced and harmonious proportions, enhancing the overall visual impact and appeal of the artwork.

How Do Artists Combine Creativity with Trigonometry to Produce Unique Artworks?

Artists combine creativity with trigonometry by using mathematical principles to guide the structure and form of their work while using their artistic vision to add unique and creative elements.

Can Trigonometry Be Found in Nature-Inspired Art? Yes, artists often use trigonometry to replicate natural patterns and structures, like fractals or spirals, which are based on mathematical principles, in their nature-inspired art.

What Are the Educational Benefits of Combining Trigonometry and Art? Combining trigonometry and art in education can enhance students’ understanding and appreciation of both subjects, showing the practical application of mathematics in creative contexts and vice versa.

Create more and better content

Check out the following resources and Grow!